How do you find the arc length and sector of a circle?
How do you find the arc length and sector of a circle?
Calculate the arc length according to the formula above: L = r * θ = 15 * π/4 = 11.78 cm . Calculate the area of a sector: A = r² * θ / 2 = 15² * π/4 / 2 = 88.36 cm² . You can also use the arc length calculator to find the central angle or the circle’s radius.
What is the relation between the arc length of a sector and the angle at the Centre of a circle?
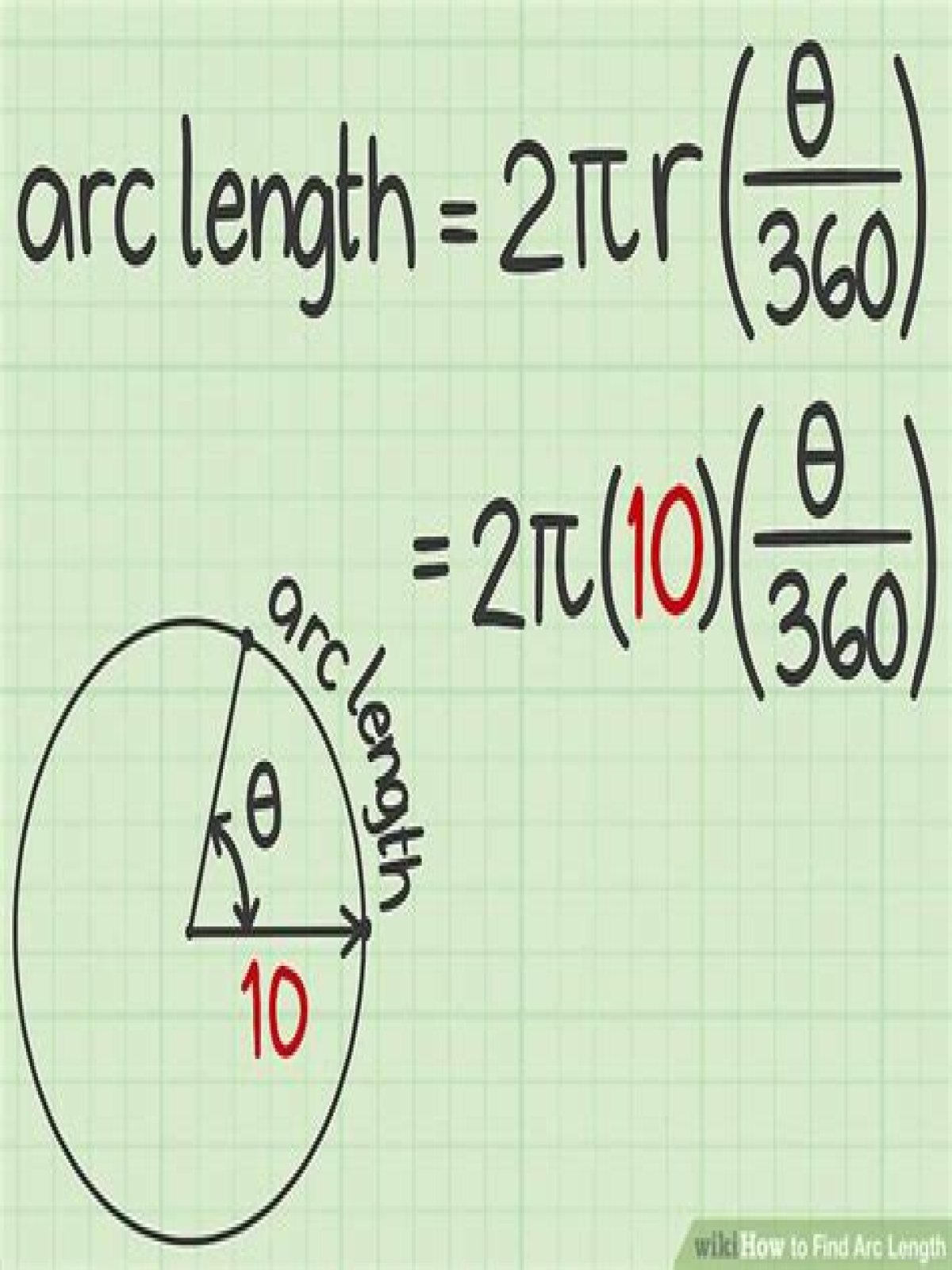
Arc length = 2πr (θ/360) θ = the angle (in degrees) subtended by an arc at the center of the circle.
How do you find the sector angle of a circle?
So, if l is the length of the arc, r is the radius of the circle and θ is the angle subtended at the centre, then; θ = l/r, where θ is in radians.
How do you find the arc length of an angle?
The arc length of a circle can be calculated with the radius and central angle using the arc length formula,
- Length of an Arc = θ × r, where θ is in radian.
- Length of an Arc = θ × (π/180) × r, where θ is in degree.
What is sector formula?
To calculate the area of a sector of a circle we have to multiply the central angle by the radius squared, and divide it by 2. Area of a sector of a circle = (θ × r2 )/2 where θ is measured in radians. The formula can also be represented as Sector Area = (θ/360°) × πr2, where θ is measured in degrees.
What is the relation between angle length of arc and radius of circle formula?
The arc length of a circle can be calculated with the radius and central angle using the arc length formula, Length of an Arc = θ × r, where θ is in radian. Length of an Arc = θ × (π/180) × r, where θ is in degree.
Is central angle equal to arc length?
The measure of an arc refers to the arc length divided by the radius of the circle. That’s why radians are natural: a central angle of one radian will span an arc exactly one radius long. …
What is the arc length of a sector?
A sector is simply part of a circle defined by two radii and an arc length. The arc length is part of the circumference ‘cut out’ by the two radii.
What is the formula for arc length of a sector?
You can find the arc length by converting the circumference formula. With a central angle in degrees, it’s 2 times pi times the radius (that’s the circumference formula) times n/360, where n is the central angle. With radians, it’s just the radius times the angle, or r*C.
How do you find the arc length of a sector?
Multiply the sector area by 2 and further, divide the result by the central angle in radians. Find the square root of the result of the division. Multiply this obtained root by the central angle again to get the arc length. The units of this calculated arc length will be the square root of the sector area units.
How to find the length of an arc and sector area?
How to find the length of an arc and sector area: an example. Calculate the area of a sector: A = r² * Θ / 2 = 15² * π/4 / 2 = 88.36 cm². You can also use the arc length calculator to find the central angle or the radius of the circle. Simply input any two values into the appropriate boxes and watch it conducting all calculations for you.
What is a sector of a circle?
A sector of a circle is a region bounded by two radii and an arc of the circle. In Figure 3 , OACB is a sector. is the arc of sector OACB. OADB is also a sector. is the arc of sector OADB. The area of a sector is a portion of the entire area of the circle. This can be expressed as a proportion.
What do you need to know about arc length and central angle?
You only need to know arc length or the central angle, in degrees or radians. The central angle lets you know what portion or percentage of the entire circle your sector is. A quadrant has a 90° 90 ° central angle and is one-fourth of the whole circle. A 45° 45 ° central angle is one-eighth of a circle.
How do you find the arc length of a circle?
Calculate the arc length to 2 decimal places. First calculate what fraction of a full turn the angle is. 90° is one quarter of the whole circle (360°). The arc length is \\ (\\frac {1} {4}\\) of the full circumference. Remember the circumference of a circle = \\ (\\pi d\\) and the diameter = \\ (2 imes ext {radius}\\).